12 июня 2020, 19:59 7 мин.

Доигрываем Лигу 1

Автор

Во Франции приняли решение завершить чемпионат и зафиксировать текущее положение команд в таблице. Решение вызвало бурную реакцию и много споров. Особенно не довольны решением Лилль и Лион, а также вылетевшие Амьен и Тулуза.

В этом материале мы попробуем смоделировать исходы несостоявшихся матчей, чтобы оценить справедливость претензий некоторых команд к решению Федерации футбола Франции.

Это решение подразумевает, что остаток чемпионата команды проведут с таким же темпом набора очков, что само по себе абсурдно, хотя бы потому, что уровень соперников в оставшихся матчах может отличаться.

Попробуем построить модель, предсказывающую результаты несостоявшихся матчей Лиги 1. В качестве базовой модели будем использовать рейтинг-систему Glicko-2, но сначала расскажем о ее предшественнице — модели Elo.

Elo

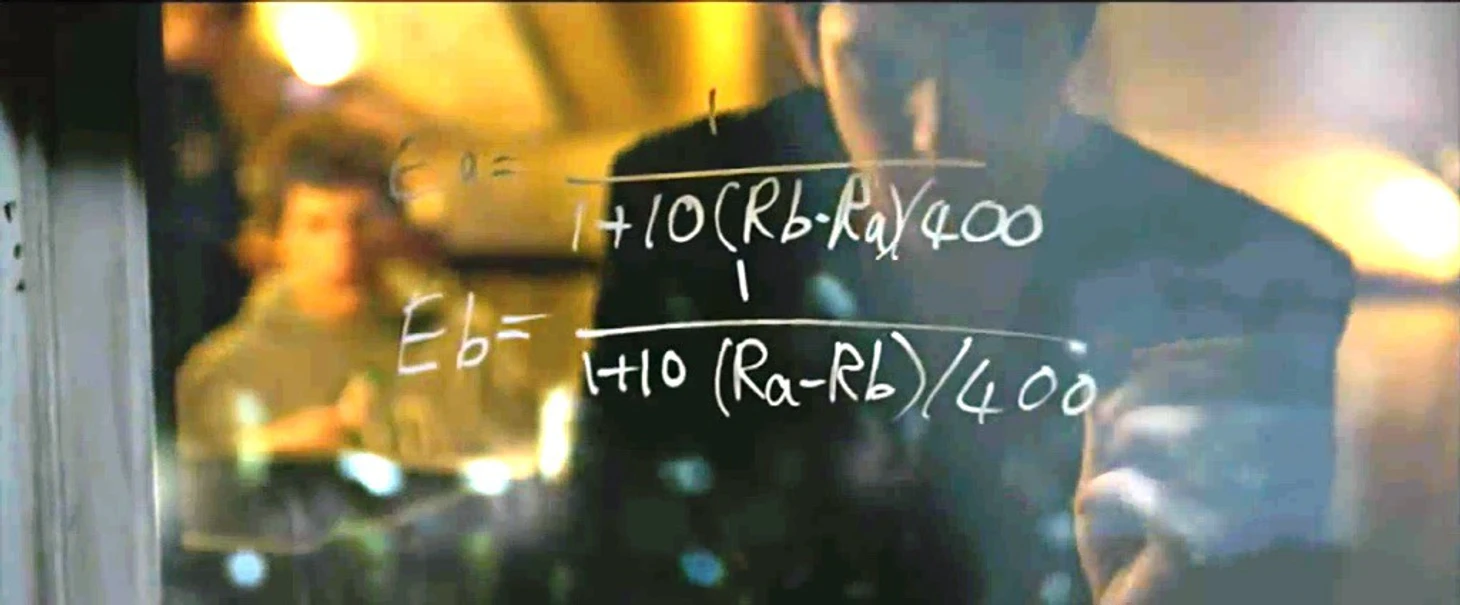
Модель была разработана в 1960 году Арпадом Эло по поручению шахматной федерации США для объективной оценки сил шахматистов.

Идея модели следующая: у каждого игрока есть рейтинг. Рейтинг – это положительное число. Чем рейтинг выше, тем игрок сильнее. Вся модель состоит из двух формул:

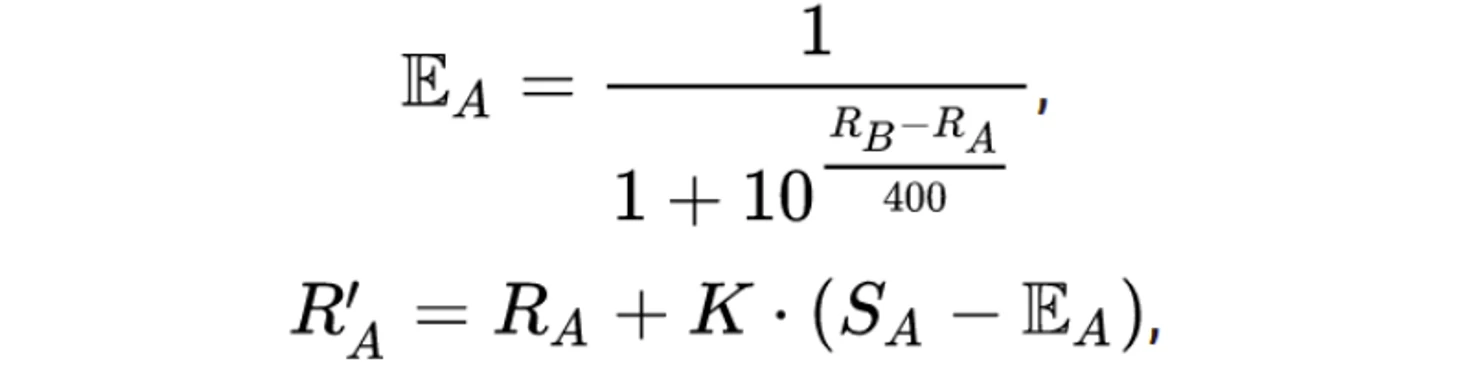
Rа , Rв - рейтинги игроков A и B.

Ea - математическое ожидание количества очков, которое наберет игрок A в матче против игрока B.

Вторая формула обновляет рейтинг Ra с учетом разницы между реальным результатом встречи игроков A и B и ожидаемым до игры результатом.

K − равен 10 для игроков с рейтингом выше 2400, 20 – для игроков с рейтингом меньше 2400 и 40 для игроков, сыгравших менее 30 сыгранных матчей.

Sa − количество очков, набранных игроком по итогу матча (1 – за победу, 0.5 – за ничью, 0 – за поражение).

Здесь нужно понимать следующее.

Ea лежит между 0 и 1; в турнирах, где нет ничьих, оно является вероятностью победы. Если рейтинги команд равны, то математическое ожидание равно 0.5.

Важно, что за победу над андердогом фаворит получает меньше баллов, чем андердог получит за победу над фаворитом. Эта логика интуитивна, потому что:

если побеждает фаворит, то оппоненты подтвердили результатом отношение своих рейтингов до игры, поэтому нет смысла существенно обновлять их рейтинги;
если побеждает андердог, то рейтинг надо существенно обновить, потому что рейтинги до игры не отображали истинного соотношения сил;
если матч заканчивается вничью, то андердог получает очки рейтинга, а фаворит теряет очки рейтинга.

Другая особенность модели — коэффициент K. Рейтинги новичков меняются быстрее, чем у игроков с богатой историей матчей: модель изначально ничего не знает о действительном рейтинге игрока, поэтому у игрока должна быть возможность быстро прийти к своему истинному рейтингу.

Glicko, Glicko-2

В 1995 году Марк Гликман (сейчас возглавляет лабораторию спортивной аналитики в Гарварде) изобретает новую модель glicko, в 2012 году появляется glicko-2.

Основное отличие моделей Гликмана от Elo состоит в том, что вводится понятие “степени доверия к рейтингу”. Эта функция заменяет коэффициент K из системы Elo. По мере накопления истории матчей, рейтинги команд меняются все меньше и меньше.

Неопределенность также вносится в математическое ожидание очков. В формуле модели заложена логика, что в матче с участием команд с небольшой историей матчей, победа аутсайдера более вероятна, чем в матче с участием более знакомых модели команд.

Модель существенно сложнее, чем модель Эло, поэтому так же подробно описывать ее не будем.

В целом, модель строится на тех же принципах, что и модель Elo, только точность Glicko-2 значительно выше.

Адаптируем Glicko-2 к футболу

Модели Elo и Glicko-2 в своем классическом виде не совсем применимы к футболу. В футболе есть ничьи, а формулы математического ожидания очков в Elo и Glicko не позволяют посчитать вероятность ничьи. Для решения этой проблемы в формулу исхода матча добавляется параметр draw_inclination, который описывает склонность команд сыграть вничью. Параметр является константой, что вообще говоря, неверно. Одни команды при равном счете готовы рисковать, чтобы вырвать победу, другие доигрывают матч более спокойно. Однако если для каждой команды завести свой параметр, то мы рискуем столкнуться с проблемой переобучения — модель не сможет адекватно предсказывать результаты будущих игр.

Во-вторых, текущие модели не учитывают фактор домашнего поля. Чтобы учесть этот признак, нужно добавить некоторое число к рейтингу домашней команды и отнять это же число от рейтинга гостевой команды перед расчетом вероятности исхода и обновлением рейтинга. После подсчета этих функций это же число отнять от домашней команды и добавить к гостевой.

Какие именно числа использовать в качестве параметров склонности к ничьей и преимущества домашнего поля? Подберем числа таким образом, чтобы точность прогноза была максимальной на результатах предыдущих 10 сезонов Лиги-1. Значения параметров, на которых получили максимальную точность, будем использовать для предсказания будущих матчей.

Прогноз будущих матчей

После подбора параметров, нам осталось лишь применить модель к текущему сезону. На основе сыгранных матчей посчитаем рейтинги команд. Это даст нам возможность посчитать вероятности исходов для оставшихся матчей. На несостоявшихся матчах запускаем метод Монте-Карло. Генерируем случайное число от 0 до 1. Если это число меньше вероятности победы, то засчитываем команде победу, если больше вероятности победы и меньше суммы вероятностей победы и ничьи, засчитываем ничью, в случае если случайное число превышает сумму вероятностей победы и ничьи, то поражение.

Результаты

Результаты можно увидеть в таблице ниже. Mp — количество сыгранных матчей. Pts, gd — количество очков и разница голов в сыгранных матчах. 1-20 — прогноз финального места для команды. В ячейках вероятности занять эти места.

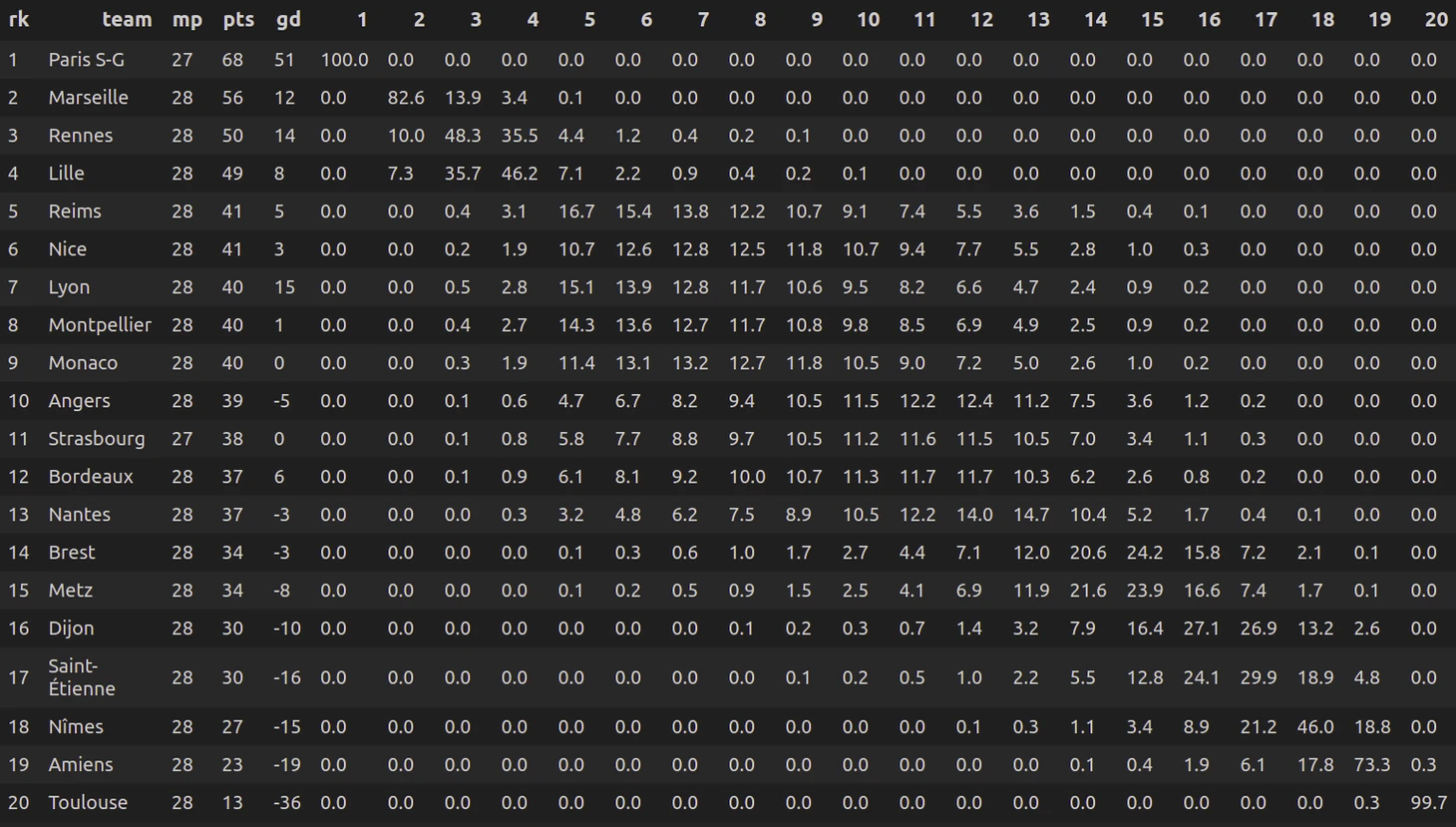
В целом текущее положение команд неплохо предсказывает “итоги” чемпионата. Однако несколько команд заслуживают внимания.

Борьба за Лигу чемпионов. Модель показывает, что Лилль имел 43-процентную вероятность ворваться в ЛЧ. Команда имеет чуть более простой календарь в оставшихся матчах (даже с учетом дополнительной игры в гостях), чем у Ренна, но преимущество в одно очко и по разнице голов ставит Ренн выше. Стоит заметить, что шансы опуститься ниже текущего четвертого места весьма малы.

Борьба за Лигу Европы. В случае победы ПСЖ в Кубке Франции и Кубке Лиги, 5 и 6 места становятся путевками в ЛЕ. Лион имеет неплохие шансы занять эти места, а места ниже текущего хуже лишь формально, поэтому Жана-Мишель Оласа понять можно.

Борьба за выживание. Тулузу могло спасти только чудо. А вот Амьен еще мог побороться.

Немного об xG (куда же без этого)

По данным Understat, Лилль и Лион уступают лишь ПСЖ по xPTS. Похоже, этим командам в предыдущих матчах везло чуть меньше.

Здесь интересно следующее. Модель, описанная выше, показывает, что календарь в оставшихся матчах у Лилля и Лиона легче, чем у прямых конкурентов. Тем не менее модель учитывает исходы матчей, но не качество игры команд. Команда может играть лучше, но проиграть, из-за чего ее рейтинг станет меньше. Модель ожидаемых голов, наоборот, никак не учитывает силу календаря, но учитывает качество игры. Таким образом, у Лилля и Лиона действительно есть повод расстраиваться из-за решения федерации.

Полагаю, нужно создать модель-гибрид из текущей модели на основе Glicko-2 и xG, но это как-нибудь потом.